基于RCM维修决策的系统可用性参数的确定

摘要  RCM是一种科学的维修理论，目前已广泛应用在军事工业和民用工业中。然而，在单一部件的可用性参数基础上如何计算系统的可用性参数是一个非常重要且被忽视的问题。为此，本文首先分析了各独立部件在RCM维修决策下的可用性参数，包括稳态可用度、稳态维修频度、平均故障间隔时间和平均停工时间、以及概率重要度等；尔后，将上述结果应用于串联系统、并联系统、表决系统等常用的可修系统，求出系统的可用性参数。

关键词  RCM、可修系统、可用性参数

0  前言

    以可靠性为中心的维修（RCM）是一种通过逻辑决断确定某产品在其使用环境下预防性维修要求的方法。在RCM中，预防性维修工作主要是由产品的故障后果决定的,并根据产品的不同故障特性，把维修工作分为保养、操作人员监控、功能检测、定时拆修、定时报废、使用检查和综合工作，而且这些维修工作都是建立在单一部件之上的。为了科学地准确地选择维修工作，有必要对每项维修工作建立数学模型，确定常用的可用性参数；另一方面，在单一部件的可用性参数基础上，如何确定系统的可用性参数也是一个重要的问题。本文的重点就在于分析解决这两个问题。

    由分析可知，保养和操作人员监控通常不需要建立数学模型。另外，在修复如新的条件下，我们可以把RCM中的定时拆修工作和定时报废工作，均可看做是定时更换维修，因此二者可采用相同的维修模型，我们称之为定时更换模型。这样，在RCM中我们研究四种维修工作模型就可以了，即功能检测模型，定时更换模型、使用检查模型和综合维修模型。

1  各项维修工作的数学模型

    符号说明

    f₁(u)、F₁(u) ：设备由完好到潜在故障的开始所用时间，随机变量u的密度分布函数和积累分布函数。

    f₂(h)、F₂(h) ：设备由潜在故障的开始到功能故障的开始所用时间，随机变量h的密度分布函数和积累分布函数。

    f(t)、F(t) ：设备由完好到功能故障开始所用时间，随机变量t的密度分布函数和积累分布函数。

    b _p ： 部件发生功能故障后的平均修复时间。

    b_f ：部件的平均预防维修时间或发生潜在故障后的平均修复时间。

    S ：检测间隔。

    S_m ：定期更换间隔。

    m，m=S_m/S：综合工作在定期更换前的检测次数。

1.1 部件的故障是明显的

1.1.1 功能检测

    设备每隔S检测一次，设备只有在运行中发生功能故障或在检测时发现潜在故障时进行修理，那么，其稳态可用度为：

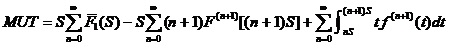
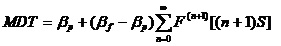
这里，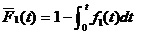

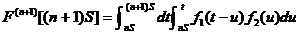
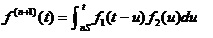
1.1.2 定时更换

    当产品工作到指定的时间S_m仍没有发生故障，则对部件进行预防维修；若部件在指定的时间S_m之前发生功能故障，立即进行事后修理。

    那么，其稳态可用度为：

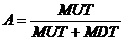
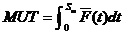
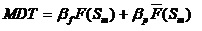
1.1.3 综合工作

    这项工作是指1.1.1功能检测工作和1.1.2定时更换工作的组合。那么，其稳态可用度为：

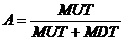
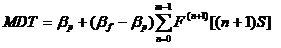
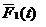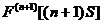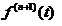        ，，见1.1.1。

1.1.4  故障更换

    产品不进行任何预防维修工作，只在发生功能故障时进行修理。那么，其稳态可用度为：

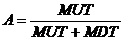
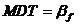
1.2 部件的故障是隐蔽的

1.2.1 使用检查

    每隔S进行一次检测，只在发现功能故障时才进行修理。那么，其稳态可用度为：

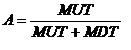
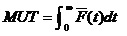
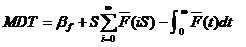
1.2.2 功能检测

    产品每隔S检测一次，产品在发现潜在故障时和功能故障时进行修理。那么，其稳态可用度为：

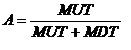
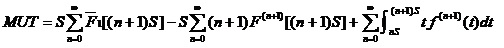
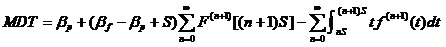
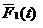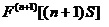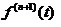    ，，见1.1.1。

1.2.3 定时更换

    无论产品是否故障，产品每隔S_m进行一次更换。

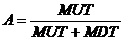
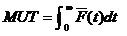
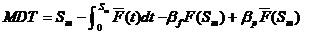
1.2.4 综合工作一

    这项工作是指1.2.1使用检查工作和1.1.3定时更换工作的组合。那么，其稳态可用度为：

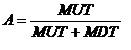
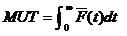
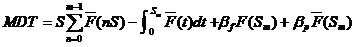
1.2.5 综合工作二

    这项工作是指1.2.2功能检测工作和1.2.3定时更换工作的组合。那么，其稳态可用度为：

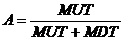
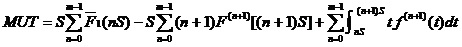
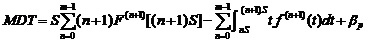
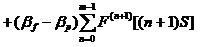
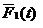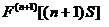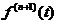     ，，见1.1.1。

2 常用的可修系统基本模型

    下面讨论工程中常用可修系统的基本模型，包括串联系统、并联系统、k/n(G)表决系统。

    假设系统由n个单元组成，所有单元之间相互独立，且修理设备足够多，即每个单元都按规定的维修策略进行修理，不存在等待修理的情况。假设第i个单元的寿命服从任意分布，平均工作时间为MUT_i ，平均停工时间为MDT_i ，（i=1,2,…, n）。假设所有单元的寿命和修理时间都相互独立，故障的单元经修理（功能故障后的修理，潜在故障后的修理，预防性维修）之后和新的一样，相当于更换。此外，由于单元可能实施预防性维修，因此单元的故障频度改称为修理频度那么，单元的稳态可用度和稳态修理频度分别为：

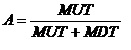       ，     i=1,2, …, n;                            （1）

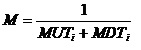       ，     i=1,2, …, n;                            （2）

    此外，注意到。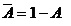

2.1 串联系统

    串联系统是：当且仅当n个单元都正常工作时系统才正常工作。系统的稳态可用度为：

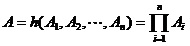
    单元i的概率重要度为：

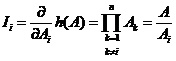
    系统的稳态修理频度为：

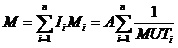
    系统的平均工作时间和平均停工时间分别为：

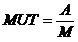
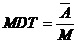
2.2 并联系统

    并联系统是：当且仅当n个单元都故障时系统才故障。系统的稳态可用度为：

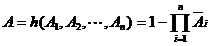
    单元i的概率重要度为：

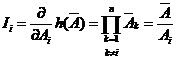           ，        i=1,2,… ,n

    系统的稳态修理频度为：

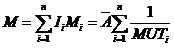
    系统的平均工作时间和平均停工时间分别为：

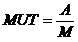
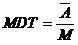
2.2 并联系统

    并联系统是：当且仅当n个单元都故障时系统才故障。系统的稳态可用度为：

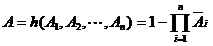
    单元i的概率重要度为：

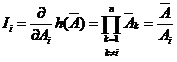
        系统的稳态修理频度为：

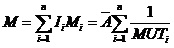
    系统的平均工作时间和平均停工时间分别为：

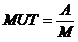
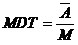
2.3 k/n(G)表决系统(1£ k£n)

    k/n(G)表决系统是：当且仅当n个单元中有大于或等于k个单元正常工作时系统才正常工作。

    系统的稳态可用度为：

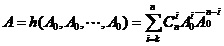
    为了对h(*)的第一个分量求导数，我们考虑：

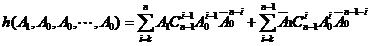
    上式右端表示：n个单元中取大于或等于k个单元正常、其它单元故障的概率，其中前一项为单元1取为正常，后一项为单元1取为故障。可得单元的概率重要度和系统的稳态修理频度为：

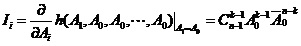        ,      i=1,2,…,n

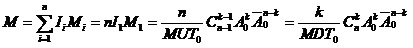
    系统的平均工作时间和平均停工时间分别为：

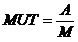
3 应用

    现在考虑一系统，其可靠性框图见图1。其中，单元A采用故障维修，单元B采用定时更换。单元C由两个子单元C₁、C₂组成，子单元C₁平时处于贮存状态，只有在C₂发生故障时才使用C₁，C₂修复后C₁又回到贮存状态，为了保证C₁的可用度，需对C₁进行定时检测。D单元为2/3(G)热贮备系统。其布函数均为威布尔分布，相应的参数见表1。子系统和系统的可用性参数的计算结果见表2。

图1

表 1

 *(2, 0.78)指的是定时更换的时间分布

表 2

     *(545.5)定时更换间隔)；*(40)定时检测间隔

4 结论

    本文讨论了可修系统可靠性模型和可用性参数体系：在单元的寿命和修理时间为任意分布的情况下，考虑了在RCM维修决策基础上的各独立单元的稳态可用性参数的计算方法，其中可用性参数包括稳态可用度，稳态修理频度，平均工作时间和平均停工时间等。在此基础上，给出了串联系统、并联系统和表决系统、等工程中常见的系统的计算方法，其结果适用于工程中出现的各种大型复杂系统。最后，举例说明了如何常用此方法进行工程计算。

参考文献

1  [英] 莫布雷 J著，石磊,谷宁昌译：以可靠性为中心的维修，机械工业出版社，1995。

2  Chister A H：(1987) Delay time model of reliability of equipment subject to inspection monitoring, Journal of Operational Research Society, 33, 723~732。

3  [英]贾尔丁A K S著，蓝文谨译：维修、更换和可靠性，机械工业出版社，1973。

4  曹晋华，程侃著：可靠性数学引论，科学出版社，1986。

5  曹晋华：可修系统可靠性研究——非指数分布模型，中国科学院应用数学研究所，1999。

EVALUATION OF THE AVAILABILITY PARAMETERS OF THE SYSTEM BASED ON RCM MAINTENANCE STRATEGIES

Luo Lifeng

ABSTRACT: RCM is a scientific maintenance theory, which has been applied widely in military industry and commercial industry. However, on the bases of the availability parameters of the single item, how to evaluate the availability parameters of the system is an important problem which has been ignored. For the sake of solving the problem, this paper evaluates the availability parameters of the single item on the basis of RCM, including stead-state availability, mean stead-state failure frequency, MTBF and MTTR, and probability importance of an item. The applications of these formulas are presented in series system, parallel system, and vote system.

KEY WORDS: RCM, repairable system, availability parameter.